문제를 보면 개별 주사위는 맘대로 회전이 가능합니다. 즉, 본인의 최솟값이 기재된 면만 보여주면 되는거죠. 주사위를 쌓은 전체 nxnxn 짜리 정육면체가 완성된다면 그냥 모든 주사위가 최솟값만 노출한다는 어찌보면 이것도 탐욕 알고리즘 기법으로 해결할수있는 문제입니다.
그러나 이 문제의 하나의 어려움?이 있다면 바로 2면, 3면을 드러내는 주사위들에 대한 최솟값 계산일겁니다. (제 생각엔)

상황설명을 위해 한번 끄적끄적 그려본 발그림입니다. 파란색 영역의 주사위는 한면만 노출하므로 그냥 최솟값을 할당하면 됩니다. 초록색과 하늘색 영역은 각각 2, 3면을 노출하므로 합이 최소인 두면, 합이 최소인 세면을 노출하면됩니다. 탐욕 기법으로 간단히 해결되지만 "전개도"<- 이게 살짝 컹스한 부분이죠. 주사위 전개도에서 인접한 두면, 세면의 합이 최소인경우를 구해주는 프로그램을 짜봅시다.
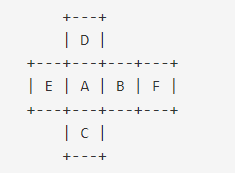
A-F까지 차례로 입력을 받습니다. 정육면체에서 나오는 인접한 두 면의 합은 총 12가지입니다. 마주보는 면을 제외하고 모든면이 인접하기때문입니다. 인접한 세면은? 얘는 8가지입니다.
사실 전체 NxNxN 도형에서 각 개별 주사위가 노출되는 양상을 보면 알겠지만 2면이 노출될땐 1개의 모서리가, 3면이 노출될땐 한개의 점(코너)을 기준으로 모인 세면이 노출되는걸 볼수있습니다. 즉, 2면이 노출되는 경우는 주사위내 모서리의 수
3면이 노출되는 경우는 주사위내 코너(꼭지점)의 수라고 볼수있죠. (그러므로 정확히는 "인접한 세면"이라는 표현은 잘못됐네요. 표현에 따르면 A,B,F도 인접한 세면이지만 코너를 포함하지 않으므로 카운트하지 않습니다.)
글로 설명하긴했지만 정육면체를 직접 그려서 생각해보면 바로 알수있습니다.

이건 계산에 쓰일 실제 1,2,3면의 분포입니다. 지면과 닿은면은 계산에 포함하지 않으므로, 다 제거해주면 2면->1면.
3면->2면으로 줄게됩니다. 결국전체 NxNxN일때 3면이 노출되는 주사위는 4개, 2면이 노출되는 주사위는 윗면에 (N-2)x4개, 기둥(?)부분 (N-1)x4개, 1면이 노출되는 주사위는 윗면에 (N-2)x(N-2)개, 옆면에 (N-2)x(N-1)x4개가 있습니다.
코딩을 한번 구상해봅시다.
입력받은 A-F값을 이용해 3개의 리스트를 만들어줍시다. 각각 1면, 2면, 3면용입니다.
각 리스트의 최솟값을 추출해 전체 주사위에서의 갯수를 곱해주면 됩니다. 아마 리스트의 길이가 길어져서 루즈해지지만
식 자체는 굉장히 간단합니다. 모든 경우의수를 리스트로 받아 무조건 최솟값만 추출하면 됩니다.
n=int(input())
a,b,c,d,e,f = map(int,input().split())
list_1 = [a,b,c,d,e,f]
list_2 = [a+b,a+c,a+d,a+e,f+b,f+c,f+d,f+e,b+d,b+c,e+d,e+c]
list_3 = [a+b+c,a+b+d,a+c+e,a+d+e,f+b+c,f+b+d,f+c+e,f+d+e]
val_1 = (n-2)*(n-2)*min(list_1)+(n-2)*(n-1)*4*min(list_1)
val_2 = (n-2)*4*min(list_2)+(n-1)*4*min(list_2)
val_3 = 4*min(list_3)
sum_val = val_1+val_2+val_3
print(sum_val)이렇게 제출했더니 띠용? 틀렸습니다!!

경우의수가 잘못입력됐나? 싶었지만 잘못된게 없습니다. 코너와 모서리의 갯수만 잘 보면 되는거니까요.
저는 혹시..? 문제가 잘못됐나 (코린이들이 흔히 빠지는 착각 "맞는데 웨 틀려요???!??"ㅋㅋ) 싶어 설마..?마사카..?
3면이 노출되는 경우에서 코너를 포함하지않는 경우 (A,B,F의 경우)도 포함되는건가? 그럴리가 없는데 싶어 계속 같은것만 제출을 했지만... 틀리더군요.
백준 알고리즘을 좀 풀어보니 제출하자마자 "틀렸습니다"라고 뜨는경우는 그냥 아예 틀린거구요
채점중 퍼센테이지가 조금 올라가다 "틀렸습니다"가 출력되는경우는 어느정도 맞았지만 뭔가 빠트린 경우더군요.
저같은경우 후자였는데요. 대체 내가 빠트린게 뭘까...? 반례가 뭘까 생각해보다가 깨달았습니다.

"val_1,2,3을 계산하는식에서 (n-2)가 포함되는데.... 그럼 n=1인 경우는...?"
생각도 못했습니다. 당연히 주사위가 산처럼 쌓여있는 그림만 생각했죠. 단일 주사위 하나 띡 놓여있는경우는 생각을 못했습니다. n=1인경우엔 a~f까지 모두 더해준다음 밑면에 최댓값을 할당해 max(list_1)을 빼주면됩니다.
n=int(input())
a,b,c,d,e,f = map(int,input().split())
list_1 = [a,b,c,d,e,f]
list_2 = [a+b,a+c,a+d,a+e,f+b,f+c,f+d,f+e,b+d,b+c,e+d,e+c]
list_3 = [a+b+c,a+b+d,a+c+e,a+d+e,f+b+c,f+b+d,f+c+e,f+d+e]
if n==1:
print(a+b+c+d+e+f-max(list_1))
else:
val_1 = (n-2)*(n-2)*min(list_1)+(n-2)*(n-1)*4*min(list_1)
val_2 = (n-2)*4*min(list_2)+(n-1)*4*min(list_2)
val_3 = 4*min(list_3)
sum_val = val_1+val_2+val_3
print(sum_val)이렇게 제출하니 맞더군요....
저의 편협한 사고때문에 고생을 꽤나했습니다. 앞으로 코딩 검증할때 경계조건들은 꼭 입력해보는걸로 해야겠습니다.
결국 전체 구조는 탐욕 알고리즘을 이용해 극단적으로 그냥 입력값을 이용해 리스트 생성후 리스트의 최댓값만 이용해 계산을 해주면 됩니다.
저는 리스트에 모든 경우의수를 다 입력했는데요.. 다른분들이 푸신것도 한번 보면서 참고해봐야겠습니다.
도형이 정육면체이므로 코너와 모서리 갯수로 처리하면 경우의수 나열하는게 마냥 어렵지는 않습니다.
Aㅏ...예전에 while While 대소문자 잘못입력해서 오류나는거 이유를 몰라서 30분가량 헤맸던 기억이 다시 떠오르네요..
앞으로 경계조건을 충실히 보겠읍니다. 그래도 골드문제였는데 크게 장애물없이 풀린것같습니다. 그냥 제 자신이 장애물이었네요.(ㅜ.ㅜ) 다음에 뵙겠습니다.
'💻 Computer Science > Algorithm🐇' 카테고리의 다른 글
| [python] 백준 1012 : 유기농 배추 (1) | 2024.01.19 |
|---|---|
| (이상한 변호사 우영우)[python] 우영우 역삼역 '회문' 판독기 (2) | 2024.01.16 |
| [python] 백준 1026 : 보물 (2) | 2024.01.14 |
| [python] 백준 11399 : ATM (0) | 2024.01.12 |
| [python] 백준 10872 : 팩토리얼 (0) | 2024.01.10 |


