KKT Condition (카루쉬-쿤-터커 최적성 조건)

KKT로 최적화 문제의 최적점을 찾아보자. KKT Condition은 말그대로 '조건'이다. 정확히는, 여러 제약조건으로 이루어진 문제의 최적점에 대한 '필요조건'이 KKT이다. "KKT를 만족하면 -> 그 점은 최적점의 후보점(Candidate)이다" 라고 말할 수 있다.
 

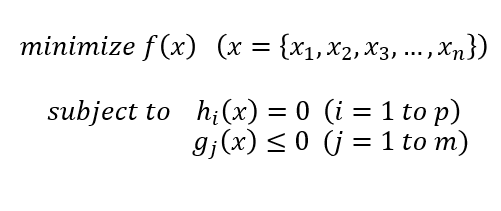
위와같은 표준형 최적설계 문제를 예로들어보자. 그전에 잠시 표준형에 대해 설명해보면, '최적점'은 결국 '극점'을 의미한다. 최댓값 혹은 최솟값을 갖는 점인데 표준형에선 최소점 (minimize f(x))으로 통일한다. (만약 최댓값을 구하는 문제면, f(x)앞에 -를 붙여준다)또한 아래 subject to 에 제약조건이 적혀있는데, h(x)는 등호제약, g(x)는 부등호 제약조건이다. 표준형에서 부등호 제약조건은 <=형태이다. 
 
쨌든, 해당 제약조건을 모두 만족하는 f(x)의 최적점을 구해보자. 어떤 방법을 써야할까? 좌표평면상 f(x)와 h(x),g(x)를 그려놓고 feasible set을 판단해 최적점을 찍는 도식해법을 쓸 수 있지만 이는 데이터의 차원이 높아질수록 플롯팅을 하기 어려워진다는 단점이있다.  직접 푸는데있어 가장 큰 이슈는 목적함수 f(x)와 제약조건 h(x), g(x)를 동시에 고려해야한다는 것이다. 심지어 제약조건은 여러개가 될 수 있다. 
이때 목적함수와 제약조건을 전부 하나의 함수로 묶어버리는 방식이 KKT이다. → 묶어버린다는게 무슨말이지? : 말그대로 목적함수와 여러개의 제약조건 함수를 선형결합하여 '하나의 함수'로 표현한다는 것이다. 그리고 이때 이 묶인 함수를 라그랑지 함수 (Lagrange function)라 한다.
 

Lagrange function과 KKT Condition

그럼 목적함수와 제약조건을 선형결합 한다했으므로 그냥 막 더해버리면 되나? → 그건 아니다. 적절한 전처리 과정이 필요하다.

라그랑지 함수의 형태이다. 위에 표준형 최적설계 문제의 목적함수는 f(x), 등호제약조건은 h(x), 부등호 제약조건은 g(x)이다. 여기서 v와 u는 라그랑지 승수(Lagrange multiplier)라 불리는 '상수'이다.(Transpose된것은 계산을위해.. 위 식의 변수는 모두 벡터이다.) 단순 선형결합 전 일종의 '가중치'를 부여하는건데 이는 제약조건이 최적해에 얼마나 영향을 미치는지 의미하는 상수로 Sensitivity의 의미를 지닌다. (제약조건에 대해 최적해가 얼마나 민감하게 반응하는가?) 라그랑지 승수가 크면 해당 제약조건이 최적해에 영향을 크게 미친다는것을 의미한다. 
그래. 그럼 v와 u가 가중치(혹은 Sensitivity)를 의미하는 상수라면, 부등호제약 함수에 더해진 s^2 텀은 뭘까? → 선형결합을 하기 위해 부등식을 그대로 끌고올 수 없다. 부등식을 =0꼴의 등식으로 변환해야 되는데 이때 <=꼴의 좌변에 적절한 상수를 더해줘 부등식을 등식으로 바꾸는 것이다. 그리고 이때 상수 s를 slack variable이라고 한다. <=꼴에 더해져 등식이 되므로 slack은 항상 양수이다. 이때 Slack이 왜 s가 아니라 s^2텀이지? → Quadratic form을 유지하기 위해! (Quadratic form은 x^T A x 꼴로 나타낼 수 있으며 이때 symmetric matrix A로 최적점에 대한 많은 정보를 알 수 있음)
정리해보면, 최적설계 문제에서 계산을 쉽게 하기위해 KKT 최적성 조건으로 최적점을 판단함. 이때 KKT는 최적설계 문제를 Lagrange function이라는 하나의 함수로 묶어버림. 묶는 과정에서 Sensitivity를 고려해 선형결합하고, 부등호 제약조건은 slack을 더해주어 등식으로 변환 후 더해줌. 이거다. 그럼 이제 Lagrange function을 만들었는데, 뭐 어쩌라고? 

 이게 KKT Condition이다. Lagrange function의 gradient가 0이 되는 지점이 최적점의 Candidate라고 판별한다. → 아하 미분해서 0되는 지점을 최적점으로 잡는다? 이건 납득할만한데 근데 뭘로 미분함?   :   전부 다. 로

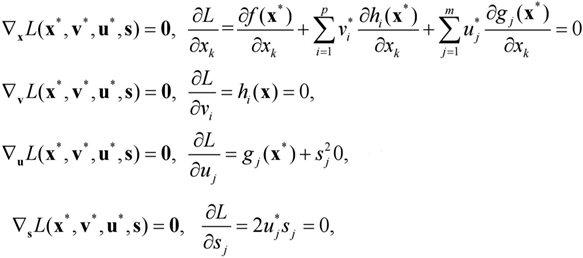
Lagrange의 설계변수 x, Lagrange multiplier v,u , slack variable s에 대한 gradient를 모두 구해준다. 그리고 그 각각의 결과가 모두 0이어야 그 점이 최적점의 candidate라는것이 KKT Condition이다. 위의 그림에서 x,v,u,s에 bold체를 넣었는데 이는 벡터를 의미하며, 실제로 설계변수든 제약조건이든 1개 이상인 경우가 많으므로 벡터 형태로 써준다.
 

KKT로 최적점을 찾는법?

그럼 실제로 최적점을 찾을때는? 저 gradient 식을 모두 연립해서 구한다. 식의 갯수는 (설계변수 갯수 + 등호제약조건 갯수 + 2*부등호 제약조건 갯수) 만큼 나올것이다. 부등호 제약조건의 경우 lagrange multiplier와 slack 이라는 2개의 변수를 창출하므로..
그럼 아마 등식이 굉장히 많이 나올것이고 연립이 어지러울것이다. (번외로, 이때 변수의갯수 = 등식의 갯수 이므로 어쨌든 연립하면 해를 구할수있다? -> 이는 선형시스템에서 통하는얘기고.. 지금은 quadratic form 즉 비선형시스템이므로.. 이에대해 확신할순없다.)
이때 연립의 시작은 제일 아래, slack에 대한 gradient로 부터 시작한다. slack은 부등호 제약조건 식에만 붙어있고, lagrange*(g(x)+slack)형태이므로 미분하면 싹다 0이 되고 2*lagrange*slack만 남을것이다. (slack은 제곱형태로 들어감으로). 무조건 2us=0의 형태가 나오는데 이를 전환조건(switching condition) 이라 한다. 무작정 연립하지않고 전환조건에서부터 연립을 시작하는데, 이때 2us=0에서 (u=0, s!=0),(u!=0, s=0), (u=0,s=0)..등 여러 케이스를 나누어 각 케이스별로 연립해 계산한다. 이때, 연립 결과 u>=0, s>=0이어야 하고, 이에 위배되는 케이스는 배제한다.