푸리에 급수, 푸리에 변환(Fourier Series, Fourier Transform)

2학년때 공수에서 배웠지만 솔직히 어디에 쓰이는지 잘 안와닿았다. 최근들어 논문을 읽기 시작하니 신호처리에서 꽤 자주FFT, FT를 이용하는 사례를 접했고 한번 정리해보는게 좋겠다 싶었다.
 
푸리에 변환을 간단히 말하면 신호를 보는 관점을 변환하는건데, 시간에 따른 진폭을 보는 일반적인 domain에서 time domain을 frequency domain으로.. 시간에 따른 이 아닌 주파수에 따른 으로 데이터를 다른관점으로 쳐다보는 방법이다.
 
프랑스의 수학자 푸리에라는 양반은 '모든 주기함수는 삼각함수의 합으로 나타낼수있다'라고 주장했다. 이 말은, 굉장히 복잡해보이는, 식을 도출하기 빡쎄보이는 '주기'함수도 우리가 흔히아는 사인, 코사인의 합으로 간단히 나타낼수 있다는것이다.  '주기성을 갖는'신호에 대해서 푸리에 급수는 신호해석에서 이점을 갖는다.
 
어떤 이점일까? 한번 눈으로 확인해보자

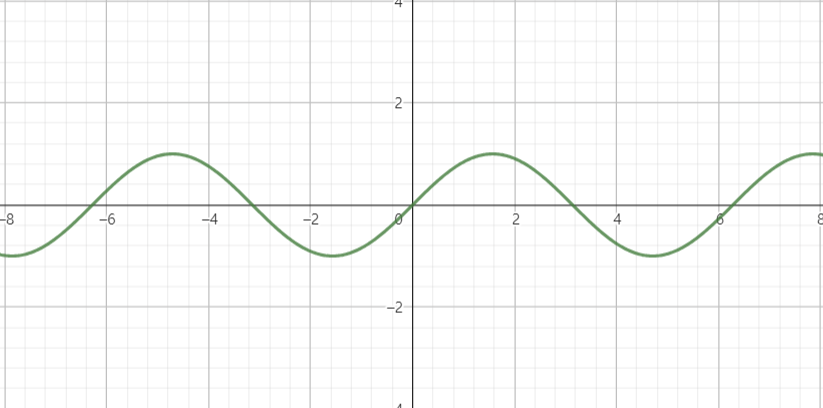
평범한 y=sin(x) 그래프 파형이다.

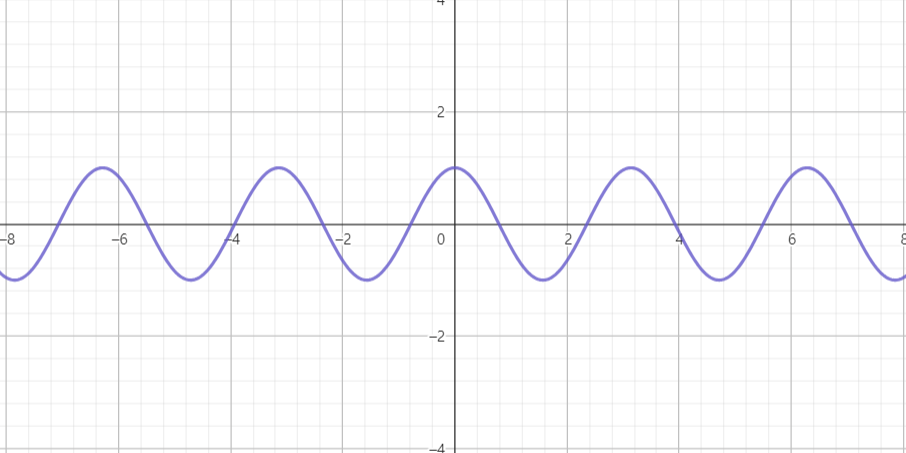
얘는 평범한 y=cos(2x) 그래프

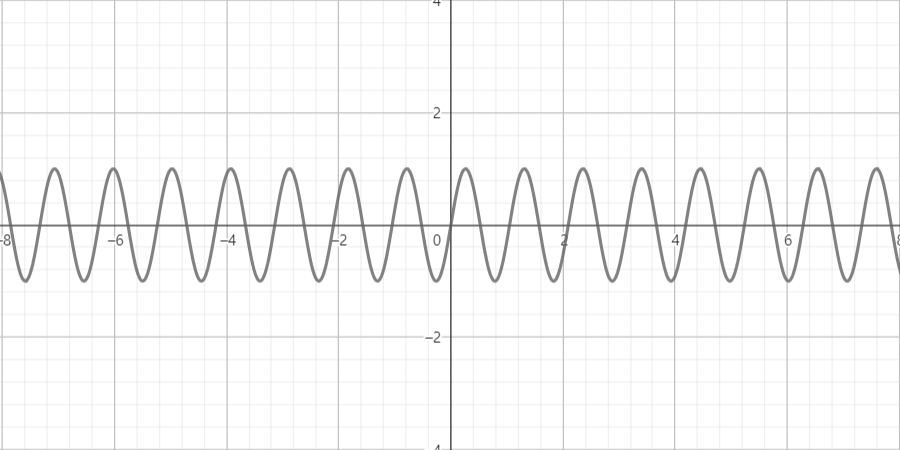
살짝 주기가 짧아졌는데, 얘는 y=sin(6x)의 그래프 파형이다. 0부터 대충 2pi에 해당하는 6.28...부근까지 파형이 6번 반복된것을 보며 짐작할수있다.

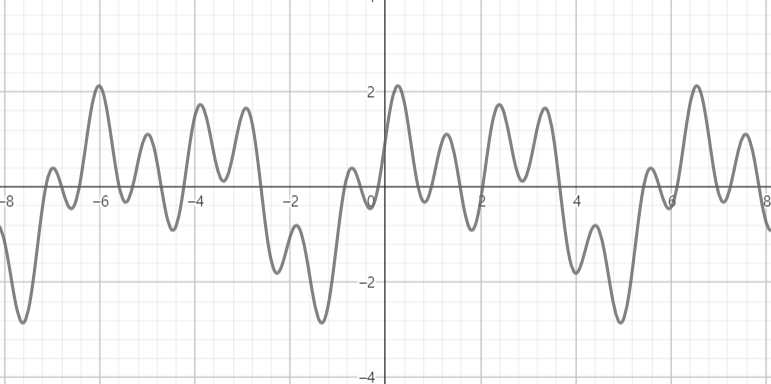
그럼 얘는 뭘까? 이 함수를 묘사할수있을까? 싶지만 얘는 위의 3개의 삼각함수를 더한 함수이다. 간단한 삼각함수 겨우 3개를 더했지만 주기가 같지않은 파형들끼리 간섭이 일어나며 모양이 상당히 곱창난것을 볼수있다. 그러나 이 함수도 주기가 있다. 주기함수들끼리 간섭이 일어났으므로 그 결과도 결국엔 주기함수이다. 
 
저렇게 복잡해보이는 함수가 사실 아주간단한 삼각함수의 합이라니, 그렇담 플롯을 저렇게 해석하는거 자체가 조금 비효율적일수도 있겠다. 여기서 '위 플롯의 식을 삼각함수의 합으로 쪼개자!'는 발상이 푸리에적 사고(?)이다. 
 

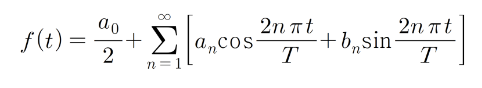
식으로 써본 푸리에 급수이다. (T는 주기) 앞에 계수 a0은 n=0일때 급수식의 값. n=1부터 코사인, 사인을 쭉 더해주는것이다. 이런식으로 주기성을 갖는 신호는 사인과 코사인의 합으로 나타낼수있다는것이다. 이때 a0, an, bn을 '푸리에 계수'라 한다.

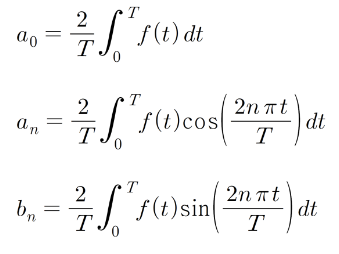
푸리에 계수는 위와같은 값을 가진다. 푸리에 계수의 유도과정은 나무위키에 잘 정리되어있으므로 참고하도록하고.. 오늘 논할것은 
'아하! 주기성을 갖는 모든함수는 '푸리에 급수'라는 사인과 코사인의 합으로 나타낼수있구나!'
 
'실제로 이 함수가 주기성은 갖지만 사인, 코사인의 합이 아니더라도! 계속 사인,코사인 더하다보면 실제 함수에 근사하고, 무한히 더하면 더더욱 근사하겠구나!'
 
이다. 대충 느낌을 알겠으니 그럼.. 푸리에 변환을 얘기해보자. 

위에 그렸던 이 함수.. time domain에선 굉장히 복잡해보인다. 근데 위에서 논했다시피 이 함수는 3종류 삼각함수의 합이다. 만약 time domain이 아닌, frequency domain에서 이 함수를 그리면 어떤식으로 그려질까? 함수의 x축이 '주파수'인 영역에서 말이야.. 
아마 이 함수를 구성하는 세 삼각함수의 주파수 지점.. 만큼 세로로 임펄스 형태로 쭉쭉 늘어난 형태일것이다. 이처럼 신호를 시간영역이 아닌 주파수영역에서 해석하는 방식을 푸리에 변환이라고 한다. 

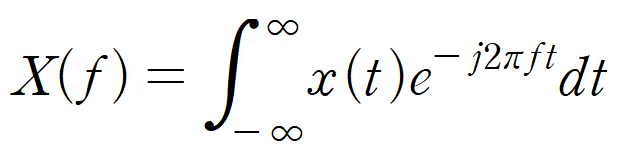
푸리에 변환 공식이다. 이걸보며 몇가지 생각할수있다.
1. 어? 위에 푸리에 급수와는 다르게 얘는 적분구간이 무한대로 정의되어있네?
-> 푸리에 변환은 푸리에 급수보다 대상이 조금더 포괄적이다. 푸리에 급수는 주기가 T인 주기함수를 대상으로 했다. 푸리에 변환은 이 주기 T를 무한대로 보내버리는것이다. 그러면 아마 세상 모든함수가 주기함수일것이다. 우리가 흔히 생각하는 '비주기 함수'가 푸리에 변환의 대상이다.
 
2. 라플라스 변환이랑 형태가 비슷한데?
-> 푸리에 변환은 라플라스 변환과 같은 적분변환 형태인데 쉽게말하면 라플라스 변환의 특별한 케이스란다. 라플라스 변환에서 경험했듯 적분변환의 이점은 time domain의 신호를 주파수영역으로 보냈다가 역변환을 이용해 다시 time domain으로 변환할수있다. 즉 time domain에서 해결못할 계산들을 변환을 이용해 주파수영역에서 해결한뒤 다시 역변환으로 time domain에 돌려놓는것이다. 
 

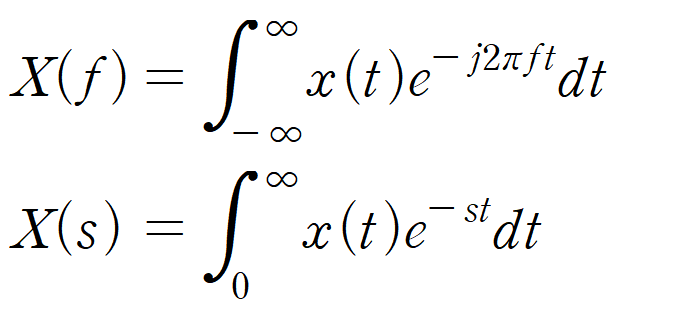
위는 푸리에 변환식, 아래는 라플라스 변환식이다. 둘다 원 함수에 복소지수함수를 곱해 쪼개서 더하는 방식이다. 이때 이 복소지수함수를 커널함수(Kernel Function)라고 한다. 두 적분변환 커널함수의 형태가 비슷해보이는데.. 둘다 커널함수가 복소지수함수 형태를 갖는 이유는 무엇일까?
가장 직관적으로, 적분계산에 강하다. 다른 함수들은 미분적분 계산을하면 형태가 난리나버리는데 비해 지수함수는 강력하다. 
또한 두 커널함수 모두 음의 지수를 갖는 지수함수이다. 적분구간이 무한대이고 감소함수이므로 커널함수와의 곱은 결국 0으로 수렴할것이다. 어떤함수가 적분변환이 가능하려면 적분결과가 수렴해야한다. 생각해보면 적분결과 발산해버리면 s-domain에서의 계산과 역변환이 컹s해질거같다. 
 
내가 공부하기위해 조금 정리해봤지만 .. 요즘은 FT를 직접 계산하는일은 잘 없기에.. (자체적으로 FFT를 해주는 센서들도 상용화되어있다) 계산법과 증명은 싹다 건너뛰고 느낌만 좀 익히기위해 글을 끄적여봤다.