선형대수 - Gauss Naive Elimination (가우스 소거법)

연립 선형대수방정식을 해결해보자. 선형대수방정식이 고차원으로 갈수록 그 해를 구하기 힘들어지는데 Gauss소거법을 이용하면 우리가 잘 아는 아주 간단한 방식으로 해를 근사할수있다.
 

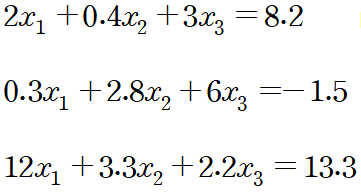
위와같은 연립 선형대수방정식이 있다. 이 해를 어떻게 구할까? 우리는 대학 선형대수 과목을 배우지않아도 이미 그 방법을 알고있다. 바로 계수를 맞추는방식으로 항을 하나하나씩 소거해나가는 방법이다. 이를 조금 체계화한게 Gauss Naive 소거법이다.
 

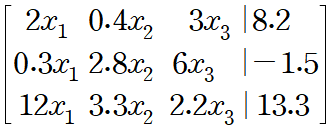
위 연립 선형대수방정식을 이렇게 행렬식으로 표현할수있다. 다소 찌그러져 보이지만 나의 부족함을 눈감아주시라.. Gauss Naive Elimination의 흐름은  일단 x3을 구한다음 차례로 x2, x1을 찾아나가는 방법을 이용한다. 이 방법을 후진대입(Back substitution)이라고한다. -> x3을 구하기위해선 한 방정식의 x1, x2항을 다 소거해야한다. x3=~ 꼴을 만들어주자. 보통은 가장 아래에있는 방정식을 이용해 x3을 구한다.  
 
한번 직접해보자

 
선이 살짝 삐뚤게 그려져서 불편하지만 그냥 보자.   처음단계는 1행과 2행만 계산해주는것이다. 첫단계의 목표는 2행의 1열 요소를 없애는것이다. 1열 요소에 계수를 맞춰 빼주면 아래와같은 결과식이 나온다. 이제 이 결과식을 행렬의 2행식으로 사용한다.

첫번째 단계인 1,2행 계산결과는 이렇게된다. 2행의 첫번째 요소가 0으로 사라졌다. 3행은 아직 건들지않았으므로 그대로이다. 
 
다음단계는? 이제 1행과 3행을 계산해주는것이다. 이런식으로 Gauss Naive Elimination은 1행으로 모든 행의 1열계수를 없애고, 2행으로 모든행의 2열 계수를 없애는.. 방식으로 간다. 일단 1행으로 3행 1열 계수도 없애보자.

아까와 같은 방식으로 1행과 3행을 계산해서 3행의 1열요소를 제거해주자. 똑같이. 아래 결과식이 3행의 자리에 들어가게된다.

1행으로 모든행의 1열을 제거한 결과이다. 이 행렬을 가지고 이제 3행의 2열을 제거해보자.

 
1행으로 한번 싹-제거된 행렬의 2,3행을 계산한 결과이다. "1열이 제거된 2행으로, 1열이 제거된 3행의 2열을 제거해준다."
표현이 다소 복잡하지만 천천히 생각해보면.. 주어진 선형대수방정식으로 만든 초기 행렬식에서.. 먼저 1행으로 모든 행의 1열을 제거한다. 이렇게되면 1행만 원본 그대로고, 나머지 행은 1열은 제거되고 나머지열도 조금씩 바뀌어있을것이다. 이 행렬을 이어서 2행으로 2행아래 모든 행의 2열을 제거한다. 이걸 마지막 열 요소만 남을때까지 반복하는것이다.
 

2,3행 계산을 마쳤을때 행렬은 위와같다. 이제 이 행렬에서 방정식의 해를 구할수있다. -35.623 x3 = 23.197이므로 x3을 구할수있고, 이 x3을 2행에 대입해 x2를 구할수있다. 이제 x3과 x2를 1행에 대입해 x1을 구하면된다. 처음에 말했듯 이 과정을 후진대입(Back substitution)이라 한다. '후진이 있으면 전진도있나요?' -> 우리가 반복하며 각 열을 지워가는 과정을 전진소거(Forward elimination)이라 한다. 결국 Gauss Naive elimination은 전진소거 후 후진대입을 하는 방법이라 할수있겠다. 

이때 행렬을 잘 보면 삼각형 모양으로 아랫부분은 영행렬이다. 위처럼 아래쪽에 위치한 삼각형모양 행렬을 하삼각행렬(Lower triangle matrix), 윗 부분 삼각형을 상삼각행렬(Upper triangle matrix)이라한다. 여기서 쓰인 Lower, Upper은 뒤에 논할 LU 분해법에 사용되므로 숙지해두면 좋다.
 
소거를 이용해 연립방정식을 푸는 방법은 중등수학에 나온 내용이다. Gauss Naive elimination은 우리가 흔히 알고있는 소거법으로 선형대수방정식을 푸는방식이다. 어렵게 생각할필요가 없다. 
 
그럼 마지막으로 이 방식의 특징을 생각해보자. 아까 1행으로 1열 요소를 없애고, 2행으로 2열 요소를 없앤다고 했는데 만약 1행으로 1열 요소를 제거할때 특정 행에서 2열요소도 제거되어버린다면? 충분히 발생할수있는 일이다. 계산되는 두 항의 계수가 각각 같다면.. 이렇게되면 계산의 어느 순간에는 0으로 나눠야하는 상황이 일어난다. 이것이 Gauss Naive elimination의 특징?허점?이다. 0으로 나누는상황에 대한 대처가 없다는것이다. 이를 방지하기위해 부분 피벗화(Partial Pivoting)를 사용한다. 
 
부분피벗화를 간략히 설명하면 방정식의 계산순서를 바꾸는것이다. 처음에 배치된 행렬의 행 순서를 바꿔주는 방식이 부분피벗화의 개념이다. 생각해보면 소거할때 계수 계산이 깔끔하게 되는 조합끼리 먼저 계산해주는것은 소거법때 많이 썼던 방식이다. 이것이 Pivoting이다.